I have never seen such a shape superimposed on a aircraft, but am not discounting it at all. But would have to ask- what are you calling " the standard formula" Are you saying there is short best short shape that is published ? I would like to know more. Sounds interesting but was interested in the actual formula as I have not seen, but always wondered if a stream line shape used for a wing strut, could be/would be expanded to total aircraft shape. I would have to toss in, that how the tail is held (wires or struts or both) Angle of tail vs wing cord angle and so many other things really would come into play...
So in really what I am saying, I am hoping it is that simple, but in reality am thinking perhaps it is not. Like you said, this is for our consideration., from the top down, I would say, this really has bearing as well. Good toss out Dan
There is an ideal streamline shape. It accounts for increased pressure if keeping the air attached in less distance, and increased skin friction for the longer shape. It is hard to keep to it in anything but fish and Blimps...
It takes work to move air around a body. The slicker the shape the less power it takes.Formulas..? You want formulas... Go here:
Below is from the car guys at EccoModding
A First Order Equation for Estimating Drag Coefficients
These are some of my thoughts and notes to give myself some understanding of the topic of how to design an economical car, how to estimate their drag coefficients, and some of the design considerations. I think you'll find it interesting. If you are bored, skip the math and look at the graphs. If you are mathematically inclined, check over my figures.
Have a look at the following
diagram.

Designing an automobile is an exercise in juggling various priorities. Note that it is possible to design a shape that gets a drag coefficient far below modern cars - the streamlined body, teardrop or icecream cone. Most cars have a Cd of around 0.35. The streamlined body has 11% the drag of a typical automobile, and at highway speeds, at least 60% of the work of an automobile is fighting this drag.
There are numerous ergonomic reasons why the teardrop shape is not optimal ergonomically. It's harder to manufacture, consumers aren't used to it, handling will not be optimal because the wheels will be required to be shorter and narrower than most cars, the trunk space will be reduced, the rear seats will have less room, etc.
However, this is a site about saving fuel. Mother nature has provided us with the teardrop shape; we have to work around that. One thing to note is that with a rake of greater than 11 degrees for the rear cone part of the icecream cone shape, there is just as much drag if not more than if it was just severed with a 90 degree bend. (Such as done with the VW 1L car).
We know that drag is primarily a function of the largest area of turbulence. Minimize turbulence completely and you are left with the a Cd of near zero - 0.04. If you have a streamlined shape up until the end (as in the above car), how big the area of that end of the car will determine largely what Cd the car has.
As such, I thought it would be useful to postulate a formula for roughly working out drag coefficients in such cars and our own modifications, relative to vehicle length so that we can get a rough idea of the optimization process and why the cars are built this way.
The first thing to do is realize that we can approximate the car as a choice between two extremes. The first of those is the half sphere. The second is the teardrop, the streamlined body, which is approximately a half sphere and a cone with 11 degree taper. (Obviously this is an approximation, but quite close.)

So, if we say that the drag should be approximately the same as the final area where we cut off the icecream cone shape, and we know that the drag has to lie between two extremes, 0.42 for the half sphere and 0.04 for the streamlined body, we can propose a formula.
Cd = 0.04 + (Af/Ahs) * 0.38
Where
Cd = drag coefficient
Af = final area at rear of car
Ahs = area of half circle (or cross sectional area of car)
Note that when Af = Ahs, we get a Cd of 0.42, which is the same as the hemisphere. And when Af = 0, we get a Cd of 0.04, as we would expect from the full streamlined body.
Next we want to get Cd in terms of l, or length from the half circle part of the car to the rear, as indicated in the above diagram. This will enable us to graph Cd versus l, give us an indication why car manufacturers make the tradeoffs they do, and give us an indication for our own car modifications.
First of all, we know that Af corresponds to the following formula for area of a circle:
Af = pi * r2 ^2
Where r2 is the radius of the final portion of the car.
If r1 = r-r2,
And since tan (theta) = opp/adj
tan theta = r1/l
therefore r1 = l * tan (theta)
therefore r2 = r - r1 = r - l * tan (theta).
Now, Af = pi * r2 ^2
= pi * (r- l * tan (theta))^2
So, Cd = 0.04 + (Af / Ahs) *0.38
= 0.04 + [(pi * (r- l * tan (theta))^2)/Ahs] * 0.38
But since Ahs = pi * r^2,
Cd = 0.04 + [(pi * (r- l * tan (theta))^2)/(pi * r^2)] * 0.38
Cd = 0.04 + [(r- l * tan (theta))^2 / (r^2)] * 0.38 So now we have a formula for drag in terms of length and radius at the widest point. Note that the above formula can be simplified in terms of (l/r) ratio. Also note that the formula will only apply with theta <=11 degrees.
If we adopt theta = 11 degrees, l/r = 5.14 gives us the full streamlined body, and l/r = 0 gives the half circle. We can now graph the result to give us a handy curve by which we know when it is appropriate to "cut off" our streamlined body.
 | This image has been resized. Click this bar to view the full image. |

Here are the same figures, but plotted against with the y-axis as logarithmic scale to give a better indication of where the diminishing returns are - around l/r = 4.

So, now we have a much better grasp on how far to extend the tail of our car in order to achieve a particular coefficient of drag, or how much we sacrifice by cutting that tail short. And note that the constants in the formula will vary from car to car, depending on how streamlined the front is, etc, but it's still good to get an overall picture of how the "boattail" thing works and the design considerations involved.
__________________
*Hucho is using Hoerner's research,and if you look at the source you find that 2.1:1 produces the lowest drag.This was from early NACA airship coastdown testing in New York.The enormous surface area of the airship envelope produced a thick turbulent boundary layer,which when sloughing off the rear tended to fill in a phantom tail area,built up from the shedding torroidal boundary layer.This dead air traveled along with the airship,effectively increasing it's L/D ratio.
*I think it was the 1929 ZMC 'tin bubble' metalclad airship which was built to one of these low ratios.It had very good speed for its power and frontal area but made the crew seasick,and you find airships built longer for flight stability.
Here's the 'tin bubble' at the bottom
 | This image has been resized. Click this bar to view the full image. The original image is sized 791x1024. |
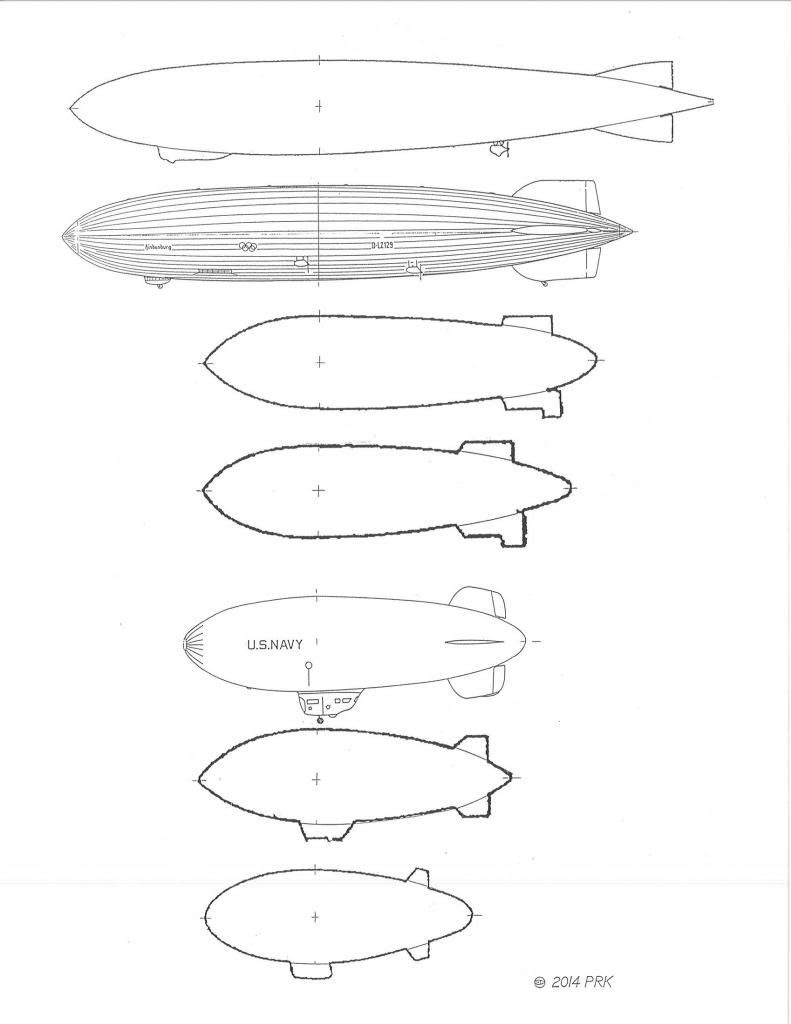
*The 2.1 ratio is low drag,but for a bluff body it exceeds Mair's 22-degree contour slope maximum and also Buchheim et al's 23-degree slope maximum.
*So as a half-body,in ground proximity,we need to stay near 22-23-degrees to protect the turbulent boundary layer from rapid pressure increases which trigger separation.
-------------------------------------------------------------------------
*For struts and airfoil sections the bottom of the friction drag/pressure drag 'bucket' occurs at L/thickness= 3.92 (also from Hoerner).So for mirror stalks,suspension fairings,wheel fairings,etc.. Also,we find that 3.92:1 has also been used successfully on record cars with plan-taper of the body only.The 1957 MG EX 181 uses it.
 | This image has been resized. Click this bar to view the full image. The original image is sized 1024x791. |

Here's the 'template',4th from bottom
 | This image has been resized. Click this bar to view the full image. The original image is sized 662x1024. |
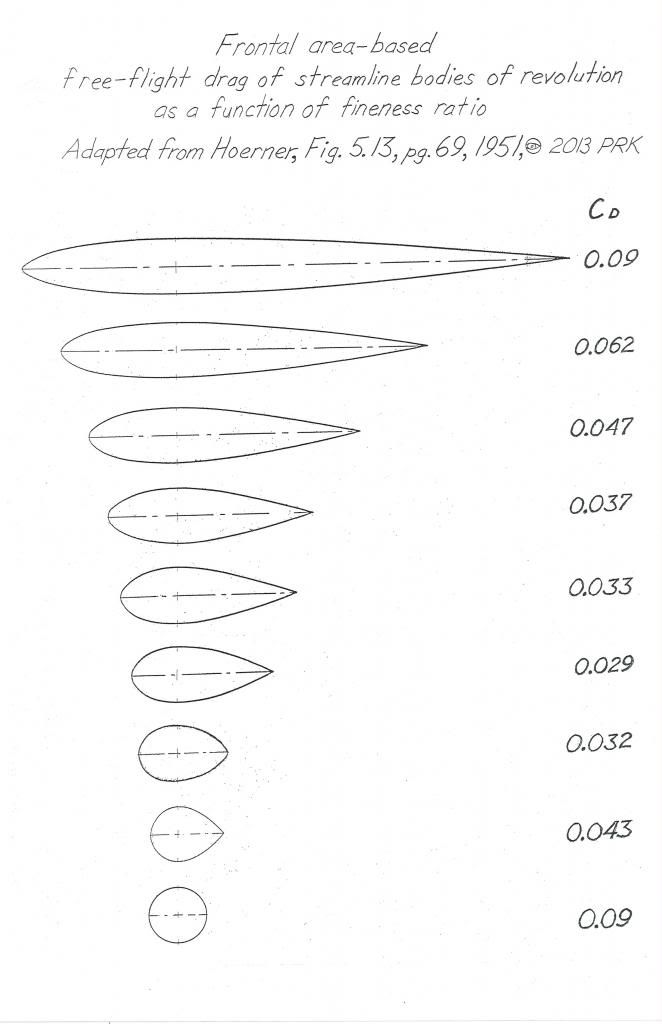
Here is the strut/wing section research,published by Horner,from Goldsein's research
 | This image has been resized. Click this bar to view the full image. The original image is sized 1000x773. |

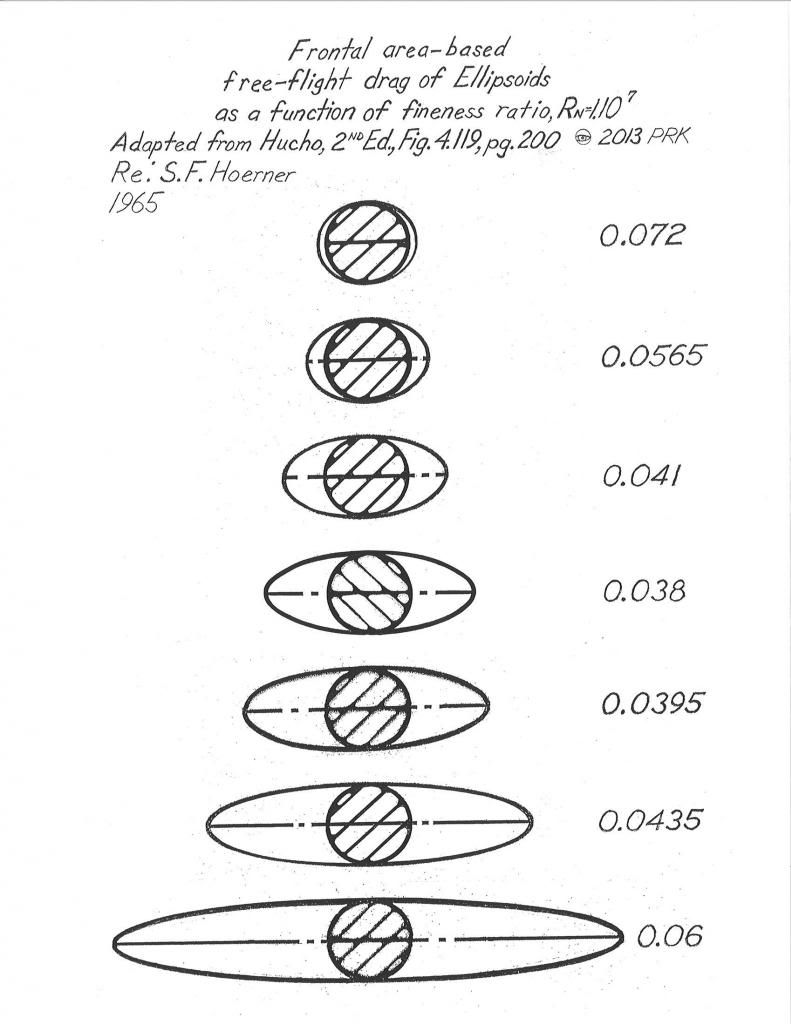
Also,we could theoretically use elliptical bodies of revolution as a basis of automobile bodies as their drag behaves exactly the same as streamline bodies EXCEPT that the windshields would be too steep to see out of,so we default to the 'bulbous','bug' nose equally low drag to get something we can see out of with glass.Hucho used the elliptical body L/D ratios in his drag example of the 1966 VW Beetle 1300,which again,show the drag minimum @ 2.5:1.
 | This image has been resized. Click this bar to view the full image. The original image is sized 791x1024. |
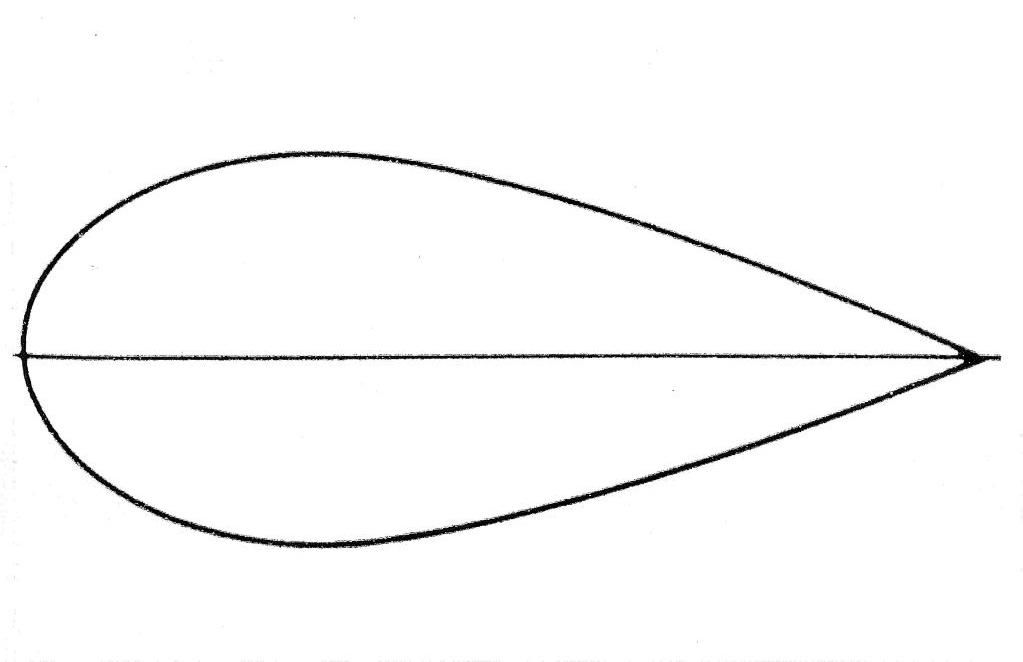
On the Aerodynamic Streamlining Template-II I used a 'faster' rear contour,closer to Buchheim et al.'s,from my college fluid dynamics text.It's close to a 2.5:1 L/D streamline body also,just a little more aggressive early in the contour,then actually more conservative at the end,with 21-degrees maximum slope.
 | This image has been resized. Click this bar to view the full image. The original image is sized 1023x662. |
Here is the Buchheim et al. contour,developed in the VW wind tunnel.We shouldn't do anything more aggressive than this or we lose the game.
 | This image has been resized. Click this bar to view the full image. The original image is sized 1024x791. |
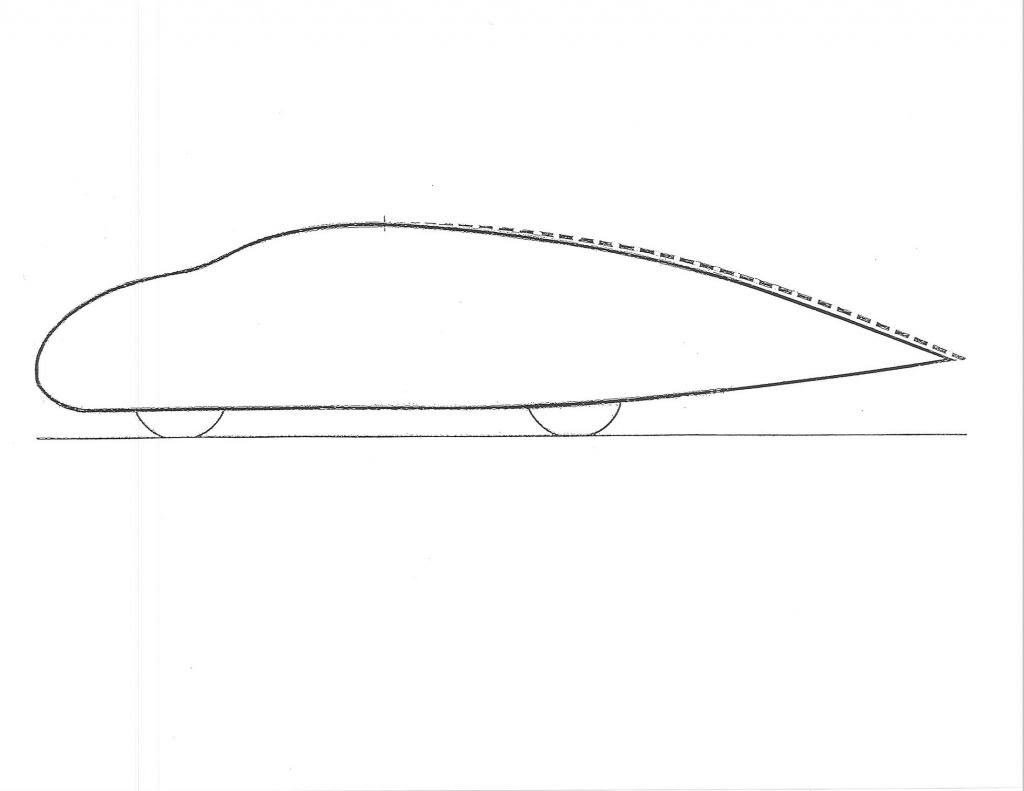
I kept the 'Template' conservative,as members are looking at maybe 800-man-hours to create an aft-body modification,and after all that you sure don't want to see separation back there.
 | This image has been resized. Click this bar to view the full image. The original image is sized 1024x791. |
